Oscar Bressan y Ana Ma. Bressan| Este problema se puede contestar fácilmente, pero a veces lleva a una conjetura falsa.
Relación entre perímetro y área de un cuadrado y un círculo. I y II parte
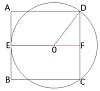
Adriana Rabino y Ana Ma. Bressan| ¿Puede tener una figura perímetro menor y área mayor que otra dada? Analicemos con los alumnos este caso tan sencillo.
Relación entre el área de un triángulo y un hexágono central interior al mismo
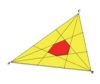
Adriana Rabino| Saber mirar y encontrar triángulos equivalentes ayuda a la solución.
Área desconocida
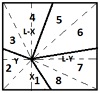
Adriana Rabino, Patricia Cuello y Marcelo Ponce| Extraído del Diario El Día| La opinión de Tenerife (www.eldia.es).
Cuadrados en un tablero de ajedrez
Oscar Bressan| El ajedrez resulta una fuente de problemas muy interesantes. En este caso, un problema de formulación muy sencilla que conecta lo geométrico con lo numérico y la búsqueda de estrategias de conteo sistemático.
Columnas de números naturales
Marcelo Ponce| Para trabajar con la paridad en N, la búsqueda de relaciones numéricas y el planteo de sucesiones aritméticas sencillas.
Dos rarezas matemáticas
Oscar Bressan| 1) Sumar un epsilón a cierto número, ¡puede traer problemas! 2) ¿Puede existir un cuerpo con volumen finito pero con superficie infinita?
Introducción a la inducción completa
Adriana Rabino| La demostración de propiedades en el conjunto de los números naturales. El Principio de Inducción Completa. Materiales: Juego de la Torre de Hanoi.
Puntos sobre una circunferencia – puntos dentro de un círculo
Oscar Bressan| Una aplicación de las ternas pitagóricas. Extensión: Puntos dentro de un círculo.
Polígonos regulares y sus propiedades utilizando como recurso el rompecabezas Zukei
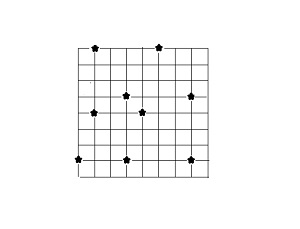
Adaptación de Adriana Rabino| En esta original actividad se proponen 42 láminas con recticulados y puntos (puzzles) donde los alumnos deben reconocer figuras geométricas pidiendo además su justificación utilizando propiedades de las mismas. Extraído...
Esperamos tus comentarios, experiencias, consultas, etc.
