Geometrizando con papel de plegado

Feb 11, 2021 | Problemas para..., Recursos para el aula, Secundaria

Marcelo Ponce y Adriana Rabino| Se promueve el estudio de las propiedades de triángulos y cuadriláteros mediante este recurso.

Dados positivos y negativos

Feb 11, 2021 | Problemas para..., Recursos para el aula, Secundaria

Adriana Rabino| Una interesante propuesta para operar con números enteros de forma lúdica.

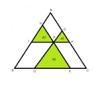
Triángulos en un triángulo

Feb 11, 2021 | Problemas para..., Recursos para el aula, Secundaria

Adriana Rabino y Marcelo Ponce| Problema para trabajar propiedades de la semejanza de triángulos y su demostración.

Templo japonés

Feb 11, 2021 | Problemas para..., Recursos para el aula, Secundaria

Oscar Bressan| Sangaku o San Gaku son tablillas de origen japonés con problemas matemáticos principalmente geométricos, creadas durante el período Edo (desde el 24 de marzo de 1603 hasta el 3 de mayo de 1868). Estas tablillas de madera se ubican en...

Cuadrados agujereados… más avanzado

Feb 11, 2021 | Problemas para..., Recursos para el aula, Secundaria

Adriana Z. Rabino, Ana Ma. Bressan y Oscar Bressan| Una versión de cuadrados con agujeros que crecen para trabajar conocimientos matemáticos del nivel medio. Se proponen actividades y sus respectivas soluciones.

Cuadrados cada vez más grandes

Feb 11, 2021 | Problemas para..., Recursos para el aula, Secundaria

Adriana Z. Rabino, Ana Ma. Bressan y Oscar Bressan| Actividades y soluciones extraídas y adaptadas de NRICH: https://nrich.maths.org/72

Los números también suben al podio

Feb 11, 2021 | Problemas para..., Recursos para el aula, Secundaria

Cristina Covas y Ana Ma. Bressan| Una manera de conectar los marcos aritmético, geométrico, algebraico y del análisis para representar números irracionales conocidos como los números metálicos de oro, plata y bronce.

¿La naturaleza sabe matemática o el hombre encuentra matemática en la naturaleza?

Feb 11, 2021 | Primaria, Problemas para..., Recursos para el aula

Adriana Z. Rabino| Para introducir a los alumnos en la sucesión de Fibonacci, y el número y el ángulo áureos de forma divertida.

Teorema de la bandera británica

Feb 11, 2021 | Problemas para..., Recursos para el aula, Secundaria

Ana Ma. Bressan| Este problema ha sido tomado del blog de Luis M. Iglesias donde se puede trabajar con una aplicación para comprobar la propiedad. Aquí se presenta completado con su demostración analítica.

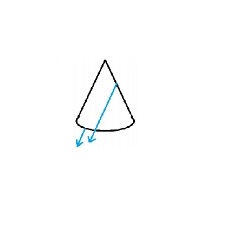
Secciones transversales en sólidos de arcilla (plastilina)

Feb 11, 2021 | Problemas para..., Recursos para el aula, Secundaria

Adriana Z. Rabino| A partir del artículo de W. Carroll: «Secciones transversales en sólidos de arcilla (plastilina)«, Arithmetic Teacher, Vol. 35 – N° 7 – Marzo 1988; N.C.T.M., Adriana Rabino ha hecho una adaptación específica de la propuesta...